Designing FIR filters for fixed-point processors, like the Atmel AVR.
This is a real problem.
Let's say you have a bandpass filter that you want to implement with 8-bit filter coefficients.
Let's say the desired filter cutoff frequencies are from 0.4 to 0.6 x π rad normalized, and you want a filter with 64 taps.
So you fire up your copy of MATLAB and do the following:
fir1(63, [0.4 0.6])
But you get coefficients like:
-4.6514e-004, 2.0622e-004, -1.9226e-004, 7.7854e-004, 1.2232e-003, -2.2140e-003, -2.5563e-003, 3.6429e-003
3.4485e-003, -3.8125e-003, -2.5674e-003, 1.2006e-003, -1.2583e-003, 4.8334e-003, 7.8943e-003, -1.2875e-002
-1.5024e-002, 1.9077e-002, 1.8249e-002, -1.8111e-002, -1.2474e-002, 5.3198e-003, -5.8078e-003, 2.0794e-002
3.6312e-002, -5.6974e-002, -7.4000e-002, 9.5467e-002, 1.1007e-001, -1.2630e-001, -1.3474e-001, 1.4079e-001
1.4079e-001, -1.3474e-001, -1.2630e-001, 1.1007e-001, 9.5467e-002, -7.4000e-002, -5.6974e-002, 3.6312e-002
2.0794e-002, -5.8078e-003, 5.3198e-003, -1.2474e-002, -1.8111e-002, 1.8249e-002, 1.9077e-002, -1.5024e-002
-1.2875e-002, 7.8943e-003, 4.8334e-003, -1.2583e-003, 1.2006e-003, -2.5674e-003, -3.8125e-003, 3.4485e-003
3.6429e-003, -2.5563e-003, -2.2140e-003, 1.2232e-003, 7.7854e-004, -1.9226e-004, 2.0622e-004, -4.6514e-004
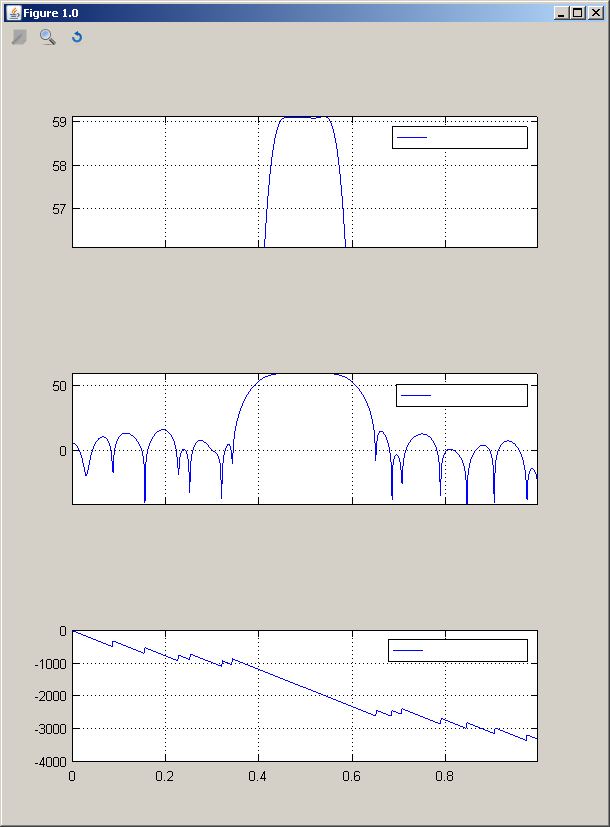
which has a reasonable filter response:

0, 0, 0, 1, 1, -2, -2, 3
3, -3, -2, 1, -1, 4, 7, -12
-14, 17, 16, -16, -11, 5, -5, 19
33, -51, -67, 86, 99, -114, -121, 127
127, -121, -114, 99, 86, -67, -51, 33
19, -5, 5, -11, -16, 16, 17, -14
-12, 7, 4, -1, 1, -2, -3, 3
3, -2, -2, 1, 1, 0, 0, 0
These coefficients provide the following filter response: