This post is an example of where trigonometry can be used in the real world and an example of how math can help you figure out what to buy. For any high school math students out there struggling to find a use for their theoretical coursework, let this be an example.
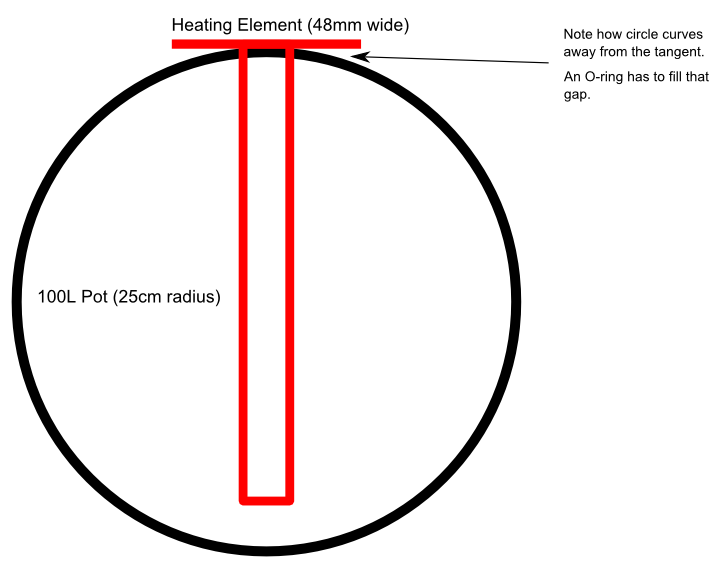
Let’s say you have a 100 liter metal pot that you want to cut a hole into, and that you want to mount a heating element to its side. The problem with drilling said hole is that water will most likely leak out of it unless you can seal the edge of the hole with some kind of flexible material, like an O-ring.
But how thick of an O-ring should you buy? O-rings have two primary dimensions, the inner diameter (I.D.) and the diameter of the ring itself, in cross-section. The O-ring has to be thick enough such that it compensates for the curve of the metal pot, as that curve “falls away” from the item you want to attach to the pot.
Here’s a picture:
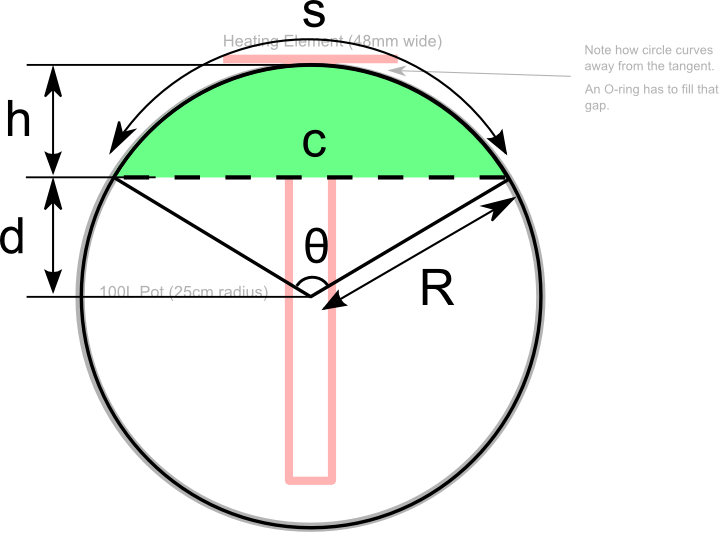
So what you’re trying to find here is the height (h) of the circular segment, given the radius of the pot (R) and the length of the heating element, which is the chord (c):
Digging into our old-school trigonometry book, the equations fall out like so:
θ = 2 arcsin (c ÷ 2R)
h = R (1 – cos (θ ÷ 2))c = 48mm
R = 250mm
In this case, we get:
θ = 11°
h = 1.15mm
So to seal the pot, an O-ring that is at least around 2mm thick would be necessary.
There’s a second problem hidden in here. When you drill a hole perpendicular to the plane tangential to the surface of cylinder representing the pot, that 3D hole will, when unfolded, be a 2D oval. In other words, the curved piece of the pot that you cut out, will become an ellipse when flattened.
You have to think about the arc length of the curve (s), which is the semi-major axis of the ellipse, because as you tighten the bolt to attach the heating element to the pot, the pot with flatten slightly, and the gaps created by the wider ellipse need to be covered by the O-ring.
In this case, the arc length of the curve (s) equals:
s = θR, where in this case θ is in radians.
s = 0.192 x 250mm = 48.049mm
In this case, the arc length is not large, meaning that the ellipse is not very eccentric, meaning that the O-ring should be quite able to cover the gaps. The proof, of course, is in the pudding, and we’ll find out how well this works when we drill the hole.