For some reason, when I was googling the Field of View (FOV) value for the Pixel 2 camera recently, I couldn’t find the answer.
So I thought back to high school trigonometry and measured it myself.
It’s not perfect, but it works:
| d_h | d_v | α_h | α_v | FOV_h | FOV_v | |
| Pixel 2 | 24.5cm | 32cm | 31.47° | 25.11° | ~63° | ~50° |
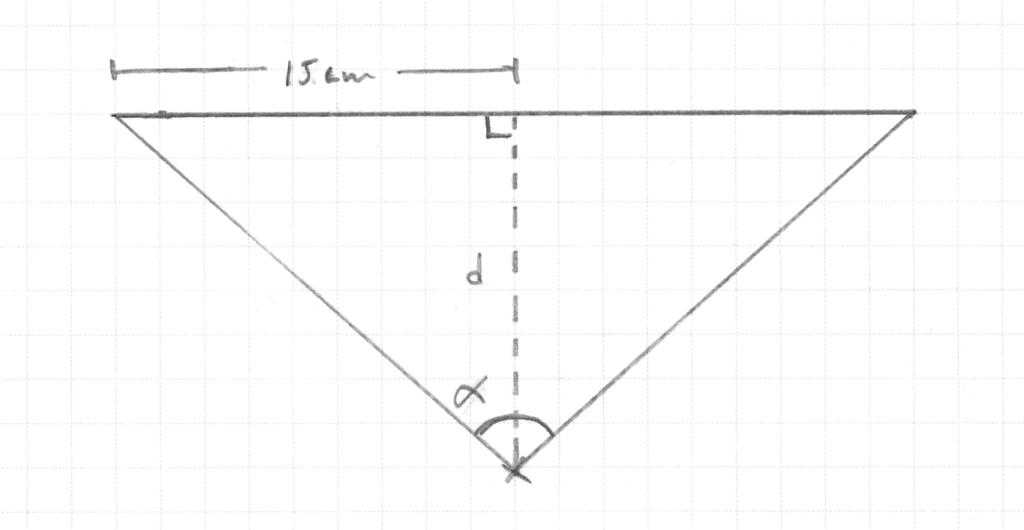
I took a 30cm ruler and taped it up, then measured how far away the camera needed to be from the ruler to fit the whole thing just inside its Field of View.
d_h = the distance away from the ruler in landscape mode
d_v = the distance away from the ruler in portrait mode
This is what it looks like:


The trigonometry for a right angle triangle means that:
α_h = arctan(15 / d_h) = arctan(15 / 24.5)
α_v = arctan(15 / d_v) = arctan(15 / 32)
and obviously the full FOV_h and FOV_v are double that.
This works with any camera, so if you don’t have the sensor size and don’t want to run through the lens equation, try this method out instead.
Finally, a practical use for all that trigonometry I memorized in high school. (Ok, that’s not true, we used a ton of it in electrical engineering, too.)
In other words, all that the Field of View triangle is saying (and indeed what the tangent ratio is saying) is that:
If we’re holding the camera in landscape mode, then stepping forwards or backwards by 24.5cm will remove or add 30cm of the scene in front of us to the picture.
If we’re holding the camera in portrait mode, then stepping forwards or backwards by 32cm will remove or add 30cm of the scene in front of us to the picture.